Block ciphers
Relevant readings: Aumasson ch. 4
What is a block cipher?
A block cipher is a type of cipher that combines a core algorithm working on blocks of data with a mode of operation, or a technique to process sequences of data blocks. More formally, a block cipher consists of two deterministic algorithms:
-
The encryption algorithm Enc takes as input a key \(k\) and a plaintext message \(m \in \Set{\texttt{0}, \texttt{1}}^*\), and outputs a ciphertext \(c\).
-
The decryption algorithm Dec takes as input a key \(k\) and a ciphertext \(c\), and outputs a message \(m \in \Set{\texttt{0}, \texttt{1}}^*\).
Usually Dec is defined as the inverse of Enc, so their corresponding implementations are similar.
Block cipher constructions
Though there are lot of block ciphers in use today, there’s only a handful of ways to construct one.
Rounds
A block cipher works by computing a sequence of rounds. A single round in a block cipher does a basic transformation that is easy to specify and implement. Putting these rounds together, we form the block cipher’s algorithm.
For example, a block cipher with three rounds encrypts a plaintext by computing \(C \gets R_3(R_2(R_1(P)))\), where the rounds are \(R_1\), \(R_2\), and \(R_3\), and \(P\) is the plaintext. The rounds must have an inverse so that it is possible to decrypt the ciphertext by computing \(P \gets R_1^{-1}(R_2^{-1}(R_3^{-1}(C)))\).
These round functions use the same algorithm, but they take an additional parameter called the round key, which means that two round functions with two distinct round keys will behave differently, and therefore will produce distinct outputs if fed with the same input.
Substitution–permutation networks
For a cipher to be considered secure, it needs to have two properties: confusion and diffusion. Confusion obscures the relationship between the key and the ciphertext as much as possible using complex transformations, and diffusion means that these transformations depend equally on all bits of the input. In the design of block ciphers, confusion is provided by substitution operations while diffusion is provided by permutation operations; when combined together they form a substitution–permutation network (SPN).
Substitution operations are done using substitution boxes, or S-boxes for short. An S-box substitutes a small block of input bits with another block of output bits using some sort of a lookup table.
One of the S-boxes used in the Data Encryption Standard (DES), namely \(S_5\), maps a \(6\)-bit input into a \(4\)-bit output as defined in the following table:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 2 | 12 | 4 | 1 | 7 | 10 | 11 | 6 | 8 | 5 | 3 | 15 | 13 | 0 | 14 | 9 | |
| 1 | 14 | 11 | 2 | 12 | 4 | 7 | 13 | 1 | 5 | 0 | 15 | 10 | 3 | 9 | 8 | 6 |
| 2 | 4 | 2 | 1 | 11 | 10 | 13 | 7 | 8 | 15 | 9 | 12 | 5 | 6 | 3 | 0 | 14 |
| 3 | 11 | 8 | 12 | 7 | 1 | 14 | 2 | 13 | 6 | 15 | 0 | 9 | 10 | 4 | 5 | 3 |
To see how this works, say we have an input 011011. It has outer bits
01 and inner bits 1101, which are \(1\) and \(13\) in decimal
respectively. The \(4\)-bit output is found by selecting the \(1\)st
row and the \(13\)th column, so the output is \(9\) or 1001 in
this case.
Permutation operations can be as simple as swapping or shuffling the bits. Some ciphers use linear algebra to permute the bits, like using a series of multiplication operations with fixed values and adding them up. Such linear algebra operations can quickly create dependencies between all the bits within a cipher and thus ensure strong diffusion.
Feistel networks
Feistel networks were first used in IBM’s block cipher called Lucifer, designed by Horst Feistel in the 1970s. Here’s a high-level description of how it works:
-
Split the \(64\)-bit block into \(32\)-bit halves \(L_0\) and \(R_0\).
-
Set \(L_1\) to \(L_0 \oplus f(R_0)\).
-
Swap the values of \(L_1\) and \(R_1\).
-
Repeat steps 2–3 fifteen times to get the values for \(L_2, \ldots, L_{16}\) and \(R_2, \ldots, R_{16}\).
-
Merge \(L_{16}\) and \(R_{16}\) into the \(64\)-bit output block.
Figure 1 visualizes this process.

The \(f\) functions each correspond to a substitution–permutation round, so they also take a round key \(K_i\). More precisely, \(f\) can be either a pseudorandom permutation or a pseudorandom function. But in a Feistel network, that difference doesn’t matter as long as \(f\) is cryptographically strong.
The number of rounds in a Feistel network depends on how strong \(f\) is. If it is strong enough, then four rounds may be enough, but real block ciphers use a lot more rounds to defend against any potential weaknesses in \(f\). DES, for example, performs \(16\) rounds.
The Advanced Encryption Standard (AES)
The Advanced Encryption Standard (AES) is the most widely-used block cipher ever. Its predecessor the Data Encryption Standard (DES), which was published in 1977, was broken in 1999 after a brute-force attack was demonstrated to be feasible in practice. Soon after, the National Institute of Standards and Technology (NIST) announced the “AES competition” to choose a successor to DES. In 2000, NIST selected a new cipher called Rijndael (pronounced like “rain-dull”) as the replacement for DES and it was standardized as AES, at which point it became the world’s de facto encryption standard.1
The internals of AES
AES processes blocks of \(128\) bits using a secret key of \(128\), \(192\), or \(256\) bits, and unlike other ciphers, AES deals with bytes. A \(16\)-byte plaintext is represented as a \(4 \times 4\) matrix (or 2D array) of bytes \(s_0, s_1, \ldots, s_{15}\): $$\begin{bmatrix} s_0 & s_1 & s_2 & s_3 \\ s_4 & s_5 & s_6 & s_7 \\ s_8 & s_9 & s_{10} & s_{11} \\ s_{12} & s_{13} & s_{14} & s_{15} \end{bmatrix}$$ More precisely, these bytes correspond to elements in the finite field of \(256\) elements \(\FF_{256}\) defined by the polynomial ring \(\FF_2[x]/\gen{x^8+x^4+x^3+x+1}\). The encryption process would then be transforming the bytes, columns, and rows of this matrix, which is possible since AES uses an SPN structure like the one shown in Figure 2.
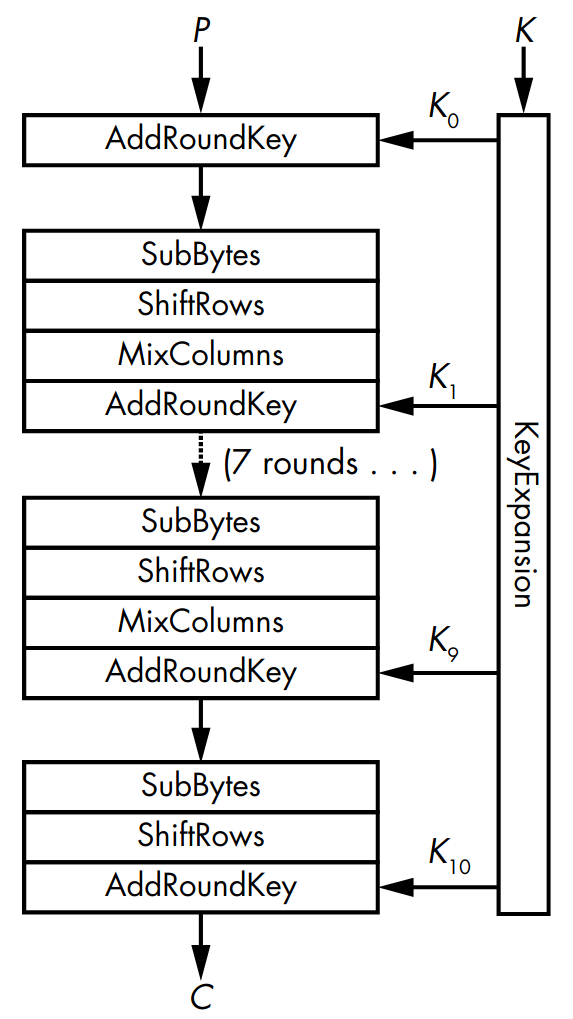
The building blocks of an AES round are:
AddRoundKey
XOR’s a round key to the internal state.
SubBytes
Replaces each byte \((s_0, s_1,\ldots, s_{15})\) with another byte
according to an S-box. In this case, the S-box is a lookup table of
\(256\) elements.
ShiftRows
Shifts the \(i\)th row of \(i\) positions, for \(i\) ranging from
\(0\) to \(3\). $$\begin{bmatrix}
s_0 & s_4 & s_8 & s_{12} \\
s_1 & s_5 & s_9 & s_{13} \\
s_2 & s_6 & s_{10} & s_{14} \\
s_3 & s_7 & s_{11} & s_{15}
\end{bmatrix}
\xrightarrow[\textsf{ShiftRows}]{}
\begin{bmatrix}
s_0 & s_4 & s_8 & s_{12} \\
s_5 & s_9 & s_{13} & s_1 \\
s_{10} & s_{14} & s_2 & s_6 \\
s_{15} & s_3 & s_7 & s_{11}
\end{bmatrix}$$
MixColumns
Applies the same linear transformation to each of the four columns of
the state. This is accomplished using matrix multiplication over
\(\FF_{256}\) where each column is multiplied by a constant square
matrix defined by $$\begin{bmatrix}
\texttt{02} & \texttt{03} & \texttt{01} & \texttt{01} \\
\texttt{01} & \texttt{02} & \texttt{03} & \texttt{01} \\
\texttt{01} & \texttt{01} & \texttt{02} & \texttt{03} \\
\texttt{03} & \texttt{01} & \texttt{01} & \texttt{02}
\end{bmatrix}$$
These operations also have inverse counterparts for the sake of decryption, namely AddRoundKey (self-inverse), InvSubBytes, InvShiftRows, and InvMixColumns.
The key scheduling algorithm is provided by the function called KeyExpansion that creates \(11\) round keys \(K_0, K_1, \ldots, K_{10}\) of \(16\) bytes each from the \(16\)-byte key. One important property of KeyExpansion is that given any round key, \(K_i\), an attacker can determine all other round keys as well as the main key, by reversing the algorithm.
Implementing AES
Unlike DES, which was originally designed to be implemented with integrated circuits, AES is designed with mainstream CPUs in mind so it is fast in software. Modern x86 processors since 2010 now have built-in instructions for encrypting and decrypting with AES, called the AES New Instructions (AES-NI), as an extension to the x86 instruction set. Most likely your computer’s CPU already supports it:
brian@thonkpad ~/classes/csci184.03
% cat /proc/cpuinfo | grep aes -m 1
flags : fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat
pse36 clflush dts acpi mmx fxsr sse sse2 ss ht tm pbe syscall nx pdpe1gb rdtscp lm
constant_tsc art arch_perfmon pebs bts rep_good nopl xtopology nonstop_tsc cpuid
aperfmperf tsc_known_freq pni pclmulqdq dtes64 monitor ds_cpl vmx smx est tm2 ssse3
sdbg fma cx16 xtpr pdcm pcid sse4_1 sse4_2 x2apic movbe popcnt tsc_deadline_timer aes
xsave avx f16c rdrand lahf_lm abm 3dnowprefetch cpuid_fault epb invpcid_single ssbd
ibrs ibpb stibp ibrs_enhanced tpr_shadow vnmi flexpriority ept vpid ept_ad fsgsbase
tsc_adjust bmi1 avx2 smep bmi2 erms invpcid rdseed adx smap clflushopt clwb intel_pt
sha_ni xsaveopt xsavec xgetbv1 xsaves split_lock_detect avx_vnni dtherm ida arat pln
pts hwp hwp_notify hwp_act_window hwp_epp hwp_pkg_req hfi umip pku ospke waitpkg gfni
vaes vpclmulqdq rdpid movdiri movdir64b fsrm md_clear serialize arch_lbr ibt flush_l1d
arch_capabilities
Instead of manually coding an AES round as a sequence of assembly
instructions, you can simply use the AESENC instruction and the CPU
will do the round for you.
PXOR %xmm5, %xmm0 ; XOR the first round key
AESENC %xmm6, %xmm0
AESENC %xmm7, %xmm0
AESENC %xmm8, %xmm0
AESENC %xmm9, %xmm0
AESENC %xmm10, %xmm0
AESENC %xmm11, %xmm0
AESENC %xmm12, %xmm0
AESENC %xmm13, %xmm0
AESENC %xmm14, %xmm0
AESENCLAST %xmm15, %xmm0 ; last round of AES
When the first x86 processors were introduced in 1978, they only have
fourteen \(16\)-bit registers, four of which are general-purpose
registers called ax, bx, cx, and dx. Each of the can be accessed
as two separate bytes (as “high” or “low” bytes), so ah corresponds to
ax’s high byte while al corresponds to ax’s low byte.
Over the years, the word size of x86 has been extended twice (the first
one was to \(32\) bits, and the second one was to \(64\) bits), and
thus also came extended registers. A \(32\)-bit register is prefixed
with an “e” so the ax register corresponds to the lowest \(16\)
bits of the eax register. Likewise, a \(64\)-bit register is
prefixed with an “r” so we have rax, rbx, and so on.
More recently, extensions to x86 such as Streaming SIMD Extensions
(SSE) and Advanced Vector Extensions (AVX) introduced even larger
registers. SSE provides \(128\)-bit registers named xmm0–xmm15,
and AVX provides \(256\)-bit registers named ymm0–ymm15 and
\(512\)-bit registers named zmm0–zmm31 from AVX-512.
Modes of operation
In this section, we present the main modes of operation used by block ciphers.
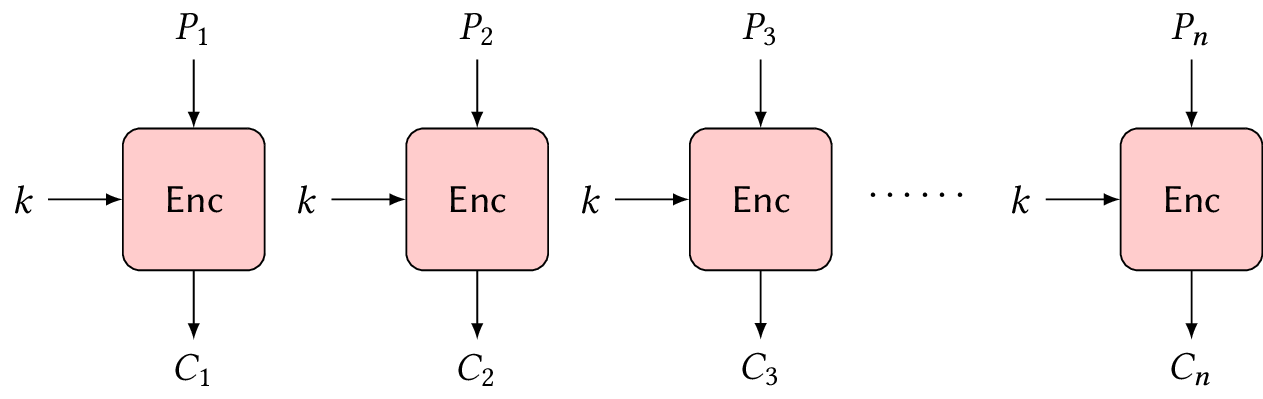
Electronic codebook (ECB)
The simplest mode is the electronic codebook (ECB). All it does is it takes blocks of plaintexts \(P_1, \ldots, P_n\) and these blocks are encrypted separately as \(C_i \gets \Enc{k}{P_i}\) for all \(i = 1, \ldots, n\), as shown in Figure 3.
It also turns out to be really insecure, and here’s why. I have an image of Tux, the Linux mascot, encrypted with a block cipher in ECB mode, and you can see the result of the encryption in Figure 4. As you can see, the patterns in the image still persist even after encryption even though the actual pixel values remain encrypted, so ECB encryption just gives you the same image but with different colors.

This is one of the iconic images in the cryptography and infosec community, as everyone who has some working knowledge of cryptography will surely have recognized this image. So if anyone asks why we shouldn’t use ECB mode, we just show them this image.2 If there’s anything to take away from this course, it’s this: never use ECB mode, ever!
Another problem with ECB mode is that it expects blocks to have the same size, so it will have trouble encrypting plaintext that does not cleanly divide into blocks of equal size unless some kind of padding is used.
Cipher block chaining (CBC)
Cipher block chaining (CBC) works like ECB, but it takes a random initialization vector (IV) which is XOR’ed with the first plaintext block, which is then fed into the encryption algorithm, and the output ciphertext block is also XOR’ed into the next plaintext block, and so on. That is, CBC encrypts the \(i\)th block as \(C_i \gets \Enc{k}{P_i \oplus C_{i-1}}\), where \(C_{i-1}\) is the previous ciphertext block. For \(C_1\), it takes the IV instead since there’s no previous ciphertext block to use.
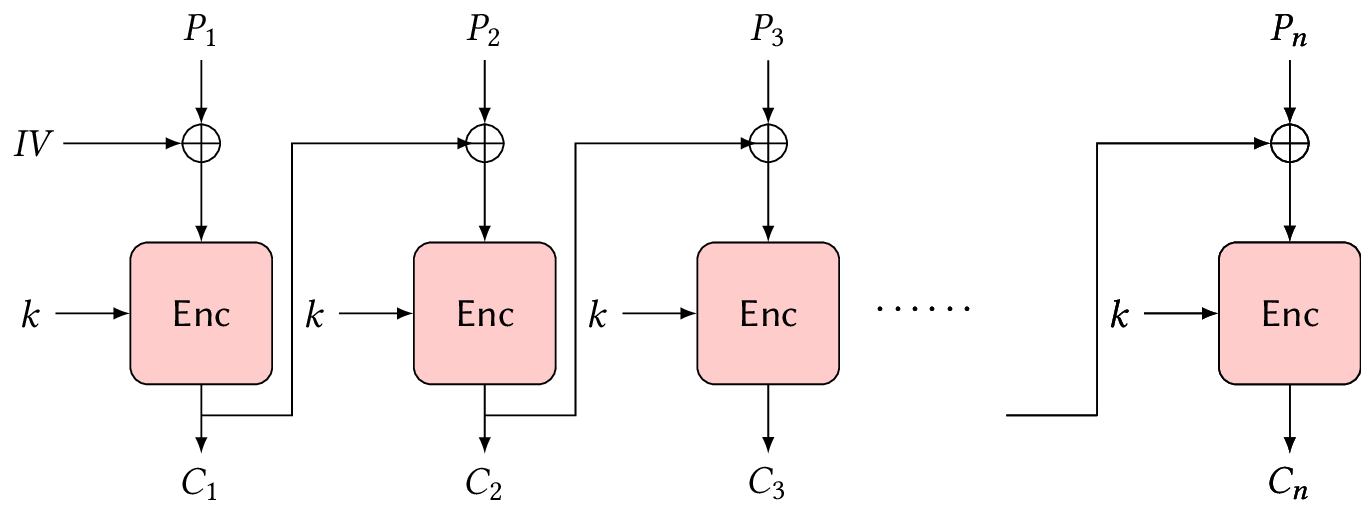
As a result, each ciphertext block is now dependent on all the previous blocks, so identical plaintext blocks won’t encrypt to identical ciphertext blocks.
Dealing with arbitrary-length data
Most of real-life data don’t split evenly into blocks. What if, for example, we want to encrypt a \(201\)-byte plaintext with AES-CBC when blocks are \(16\) bytes? What do we do with the leftover \(9\) bytes? There are two ways to deal with this problem:
-
Padding
Make the ciphertext a bit longer than the plaintext.
-
Ciphertext stealing
Produce a ciphertext of the same length as the plaintext.
Padding appends extra bytes at the end of the leftover block to fill a complete block. One such padding scheme is the PKCS#7 standard, which is the most widely used for block ciphers. For a block size of \(16\) bytes, it works like this:
-
If there’s one byte left, pad the message with \(15\) bytes
0f(which is \(15\) in decimal). -
If there’s two bytes left, pad the message with \(14\) bytes
0e(which is \(14\) in decimal).
And so on. If the length of the original message is already a multiple
of \(16\), we pad it with a whole block of 10 (which is \(16\) in
decimal). This seems simple enough to do it in Python:
def pkcs7_pad(p, blklen=16):
n = blklen - (len(p) % blklen) # find number of bytes to pad
pad = bytes([n] * n) # generate the extra bytes
return p + pad # and add it to the end
Then we try it for some arbitrary-length bytestrings:
>>> pkcs7_pad(b'This is getting padded!', 26)
b'This is getting padded!\x03\x03\x03'
>>> pkcs7_pad(b'this has 16bytes')
b'this has 16bytes\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10'
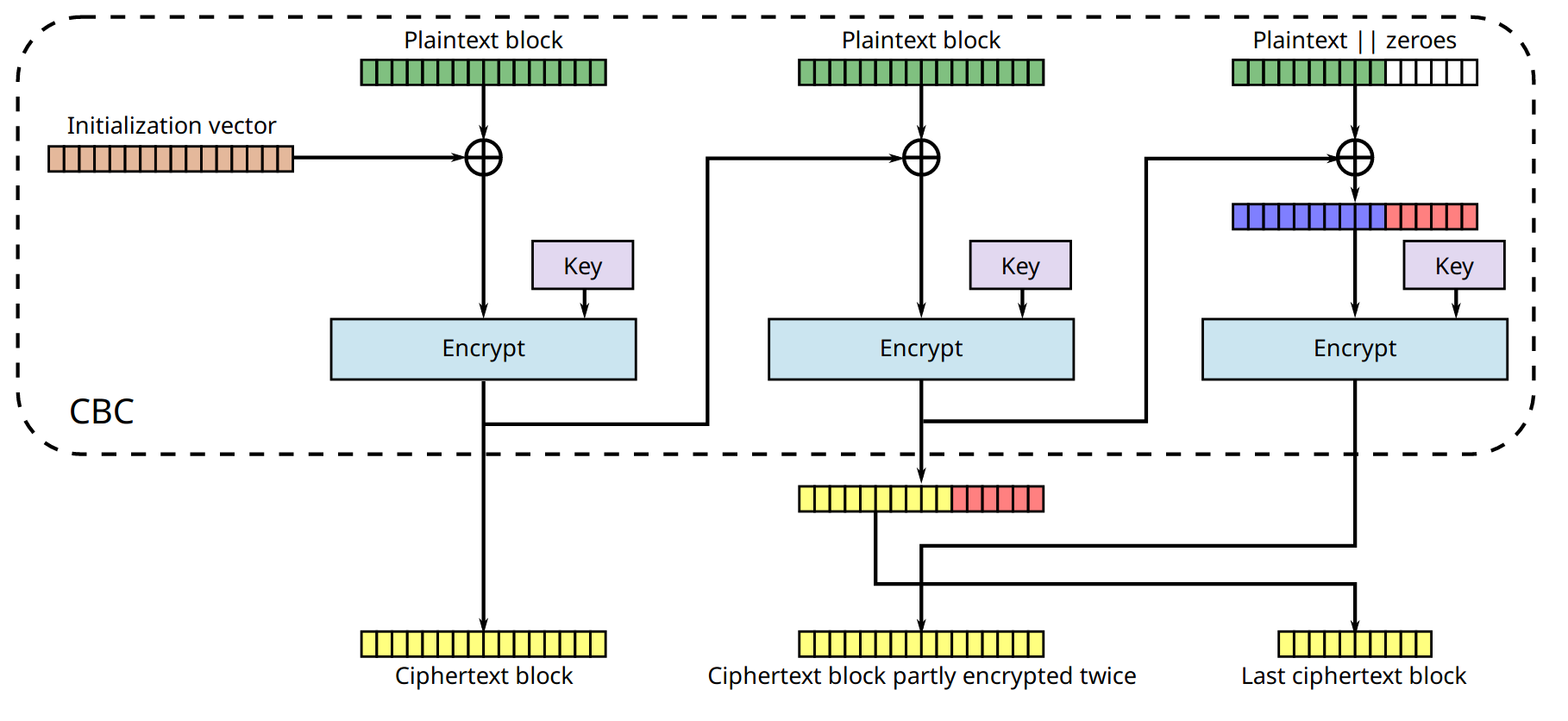
Another method, though less popular than padding, is ciphertext stealing. Its advantage over padding is that it can deal with plaintexts of any bit length, not just bytes, and that ciphertexts are exactly the same length as plaintexts. More importantly, CBC with ciphertext stealing is resistant to padding oracle attacks (we’ll talk about this later).
Figure 4 shows the process of ciphertext stealing in CBC mode. Here, ciphertext stealing extends the last incomplete plaintext block (shown in blue) by “stealing” bits from the previous ciphertext block (shown in red), and then encrypts the resulting block. The last, incomplete ciphertext block is made up of the first blocks from the previous ciphertext block (shown in yellow); that is, the bits that have not been appended to the last plaintext block.
Counter (CTR) mode
The counter mode is a bit weird among other modes of operation, since this mode essentially turns a block cipher into a stream cipher. It uses the encryption algorithm of the block cipher to generate the keystream, which will then be used to actually encrypt the plaintext, as seen in Figure 5.
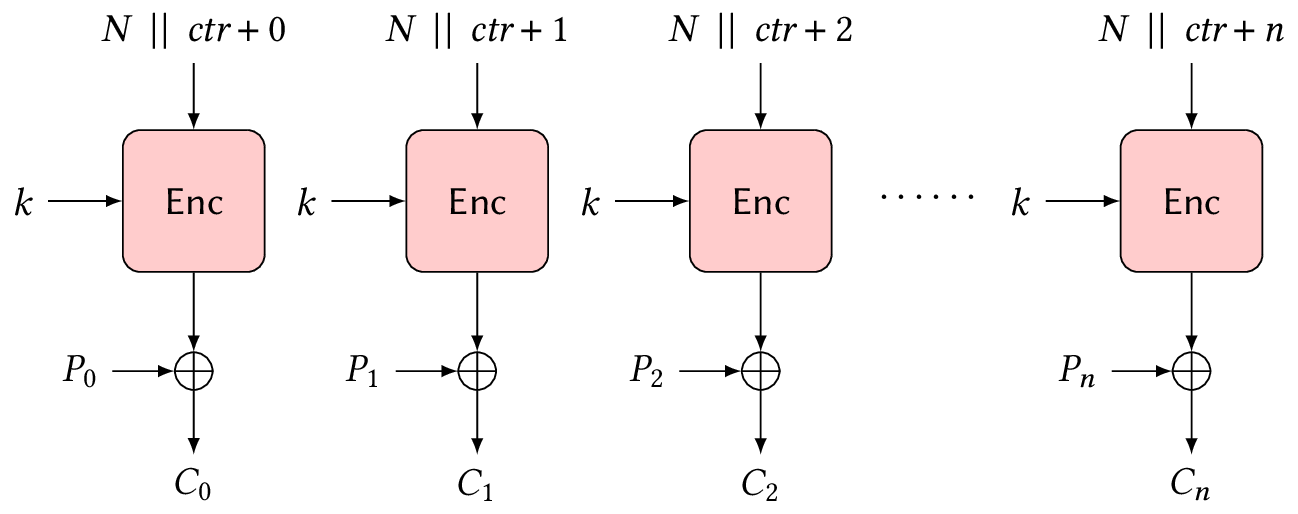
More specifically, it will encrypt blocks composed of a counter \(\textit{ctr}\), which is an integer that is incremented for each block, and a nonce \(N\), so the \(i\)th keystream block is generated by \(K_i \gets \Enc{k}{N \mathrel{\hspace{1pt}||\hspace{1pt}}\textit{ctr}+i}\) and the actual encryption is done by computing \(C_i \gets P_i \oplus K_i\) for \(i = 0, 1, \ldots, n\). Keep in mind that a nonce should not be reused to encrypt two different messages.
One advantage of CTR mode is that it can be faster than in any other mode, since it is parallelizable (i.e., each block does not depend on another in any way). Also, because CTR mode is just a glorified stream cipher, you can start encrypting the plaintext as it is being sent even without having the entire plaintext available from the start.
Other modes of operation
Aside from ECB, CBC, and CTR modes, we also have output feedback (OFB) and cipher feedback (CFB) modes, which nobody really uses in practice. There are also modes of operation for specific applications, such as Galois/Counter Mode (GCM) and counter with CBC-MAC (CCM) for authenticated encryption.
Padding oracle attacks
One of the best-known attacks in modern cryptography are padding oracle attacks. Although it was discovered in the 2002 by academic cryptographers and then ignored for some time, it was rediscovered a decade later when it was found out that SSL and web frameworks like Ruby on Rails and ASP.NET were vulnerable and by that time these attacks were demostrated to be practical.3
A padding oracle is a magical thing (usually comes in the form of a black box or an API) that can tell whether or not the padding in a CBC-encrypted ciphertext is valid. In practice, a padding oracle can be found in a service on a remote host sending error messages whenever it receives malformed ciphertexts.4 Padding oracle attacks keep track of inputs that have a valid padding and those that don’t, and exploit this information to decrypt chosen ciphertext values.
Suppose we want to decrypt the ciphertext block \(C_2\), like the one shown in Figure 6. We’re looking for some value \(X\), which is \(\Dec{k}{C_2}\), and \(P_2\), the block obtained after decrypting in CBC mode. If we pick a random block \(C_1\) and send the two-block ciphertext \(C_1 \mathrel{\hspace{1pt}||\hspace{1pt}}C_2\) to the oracle, decryption will only succeed if \(C_1 \oplus P_2\) ends with a valid padding (following the PKCS#7 standard).
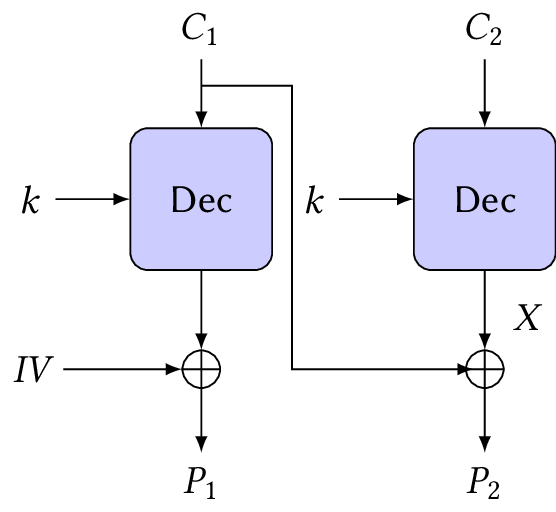
For convenience, we’ll introduce here the array notation for bytes, where \(X[0]\) is the first byte, \(X[1]\) the second, and so on. Padding oracle attacks on CBC encryption can decrypt a block \(C_2\) like this:
-
Pick a random block \(C_1\) and tweak its last byte until the padding oracle accepts the ciphertext as valid.
If the ciphertext is valid, then \(C_1[15] \oplus X[15] = \texttt{01}\).
-
Find the value \(X[14]\) by setting \(C_1[15]\) to \(X[15] \oplus \texttt{02}\) and searching for the \(C_1[14]\) that gives a correct padding.
When the padding oracle accepts the ciphertext as valid, it means we have a value for \(C_1[14]\) such that \(C_1[14] \oplus X[14] = \texttt{02}\).
-
Repeat steps 1 and 2 for all \(16\) bytes.
References
- Aumasson, Jean-Philippe. 2017. Serious Cryptography: A Practical Introduction to Modern Encryption. No Starch Press.
This is why I chose this as the icon for our Discord server, and also in the home page of this course on Canvas.
This is one of those cases when error messages can reveal too much information, like having a specific error when the padding is invalid.