Hash functions

Relevant readings: Aumasson ch. 6, Wong ch. 2

Hash functions

If you recall your CSci 30 class, a hash function maps an arbitrary-size input to a fixed-size output called a hash or digest. The usual application for these is for hash tables, a data structure that allows constant-time lookups.

Due to the pigeonhole principle,¹ all hash functions are susceptible to hash collisions, where two different inputs can hash to the same output. To mitigate this, hash functions should be carefully constructed such that the probability of a hash collision occurring is as negligible as possible.

Cryptographic hash functions

Not all hash functions can be used for cryptographic applications. Checksum algorithms such as CRC-32 (as you have seen from Homework 2) are not designed with security in mind, thus making them unsuitable as cryptographic hash functions. For example, the WEP protocol from the IEEE 802.11 standard used CRC-32 as part of checking message integrity that eventually rendered it insecure, partly due to the linearity property that CRC-32 has.

A cryptographic hash function can be defined in terms of security notions, sorted from weakest to strongest:

1. Preimage resistance

   Given \(y = H(x)\) for a uniform \(x\), it is infeasible for a PPT adversary to find a value \(x^\prime\) (whether equal to \(x\) or not) such that \(H(x^\prime) = y\).

   In other words, \(H\) is a one-way function.

2. Second preimage resistance

   Given a uniform \(x\), it is infeasible for a PPT adversary to find a second preimage \(x^\prime \ne x\) such that \(H(x^\prime) = H(x)\).

3. Collision resistance

   It is infeasible for a PPT adversary to find distinct \(x, x^\prime\) such that \(H(x) = H(x^\prime)\).

Collision resistance

Since hash collisions are unavoidable, the next best thing we can do is to make generating such collisions infeasible, i.e., hard to find.

The following definition is for keyed hash functions:

Consider the HASH-COLL game:

1. A key \(s\) is generated by running \(\Gen{\texttt{1}^n}\).

2. The adversary \(\mathcal{A}\) is given \(s\), and outputs \(x, x^\prime\).

3. \(\mathcal{A}\) wins if and only if \(x \ne x^\prime\) and \(H^s(x) = H^s(x^\prime)\). In such a case, we say that \(\mathcal{A}\) has found a collision.

Security considerations (taken from (Wong 2021))

So far, we saw three security properties of a hash function: preimage resistance, second preimage resistance, and collision resistance. These security properties are often meaningless on their own; it all depends on how you make use of the hash function. Nonetheless, it is important that we understand some limitations here before we look at some of the real-world hash functions.

First, these security properties assume that you are (reasonably) using the hash function. Imagine that I either hash the word “yes” or the word “no,” and I then publish the digest. If you have some idea of what I am doing, you can simply hash both of the words and compare the result with what I give you. Because there are no secrets involved, and because the hashing algorithm we used is public, you are free to do that.

And indeed, one could think this would break the preimage resistance of the hash function, but I’ll argue that your input was not “random” enough. Furthermore, because a hash function accepts an arbitrary-length input and always produces an output of the same length, there are also an infinite number of inputs that hash to the same output.

Again, you could say, “Well, isn’t this breaking the second preimage resistance?” Second preimage resistance is merely saying that it is extremely hard to find another input, so hard we assume it’s in practice impossible but not theoretically impossible.

Second, the size of the digest does matter. This is not a peculiarity of hash functions by any means. All cryptographic algorithms must care about the size of their parameters in practice. Let’s imagine the following extreme example.

For this reason, there is a minimum output size that a hash function must produce in practice: \(256\) bits (or \(32\) bytes). With this large an output, collisions should be out of reach unless a breakthrough happens in computing.

Certain constraints sometimes push developers to reduce the size of a digest by truncating it (removing some of its bytes). In theory, this is possible but can greatly reduce security. In order to achieve \(128\)-bit security at a minimum, a digest must not be truncated under \(256\) bits for collision resistance, or \(128\) bits for preimage and second preimage resistance. This means that depending on what property one relies on, the output of a hash function can be truncated to obtain a shorter digest.

Hash functions in practice

Merkle–Damgård construction

The Merkle–Damgård construction is essentially a way to turn a secure compression function that takes small, fixed-length inputs into a secure hash function that takes inputs of arbitrary lengths.

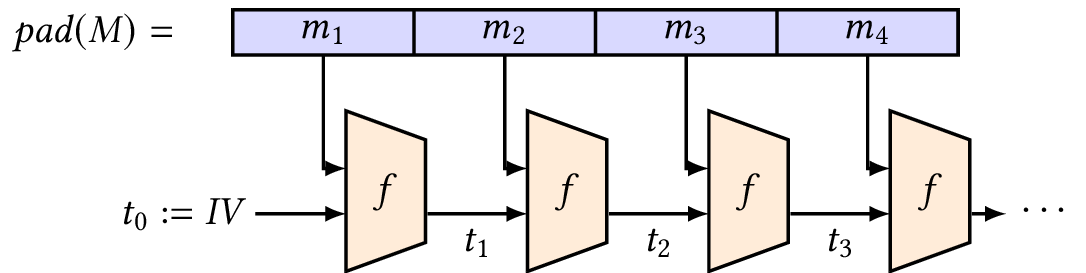
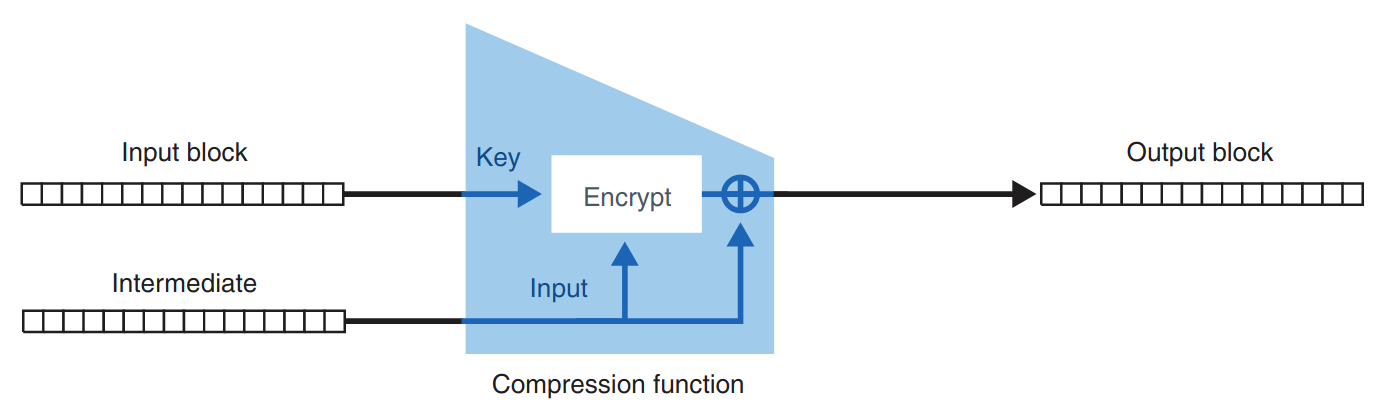
A compression function takes two inputs of some size and produces one output of the size of one of the inputs. Put simply, it takes some data and returns less data. While there are different ways of building a compression function, SHA-2, for example, uses the Davies–Meyer construction (see Figure 1), which relies on a block cipher.

First, it applies a padding to the input we want to hash, then cuts the input into blocks that can fit into the compression function. Cutting the padded input into chunks of the same block size allows us to fit these in the first argument of the compression function. For example, SHA-256 has a block size of \(512\) bits.

Second, it iteratively applies the compression function to the message blocks, using the previous output of the compression function as second argument to the compression function. The final output is the digest.

SHA-3 and the sponge construction

Both the MD5 and SHA-1 hash functions were broken somewhat recently. These two functions made use of the same Merkle–Damgård construction described in the previous section. Because of this, and the fact that SHA-2 is vulnerable to length-extension attacks, NIST decided in 2007 to organize an open competition for a new standard: SHA-3.

In 2007, 64 different candidates from different international research teams entered the SHA-3 contest. Five years later, Keccak, one of the submissions, was nominated as the winner and took the name SHA-3. In 2015, SHA-3 was standardized in the NIST publication FIPS 202.²

SHA-3 is built with a sponge construction, a different construction from Merkle–Damgård that was invented as part of the SHA-3 competition. This is a relatively new way to construct hash functions, since it is built on top of a permutation instead of a compression function. Instead of using a block cipher to mix message bits with the internal state, sponge functions just do an XOR operation. Sponge functions are not only simpler than Merkle–Damgård functions, they’re also more versatile. You will find them used as hash functions and also as deterministic random bit generators, stream ciphers, pseudorandom functions, and authenticated ciphers.

To use a permutation in our sponge construction, we also need to define an arbitrary division of the input and the output into a rate \(r\) and a capacity \(c\). Where we set the limit between the rate and the capacity is arbitrary. Different versions of SHA-3 use different parameters. We informally point out that the capacity is to be treated like a secret, and the larger it is, the more secure the sponge construction.

A sponge function works as follows:

1. It XORs the first message block \(m_1\) to a predefined initial value of the internal state (for example, the all-zero string). Message blocks are all the same size and smaller than the internal state.

2. A permutation \(f\) transforms the internal state to another value of the same size.

3. It XORs block \(m_2\) and applies \(f\) again, and then repeats this for the message blocks \(m_3\), \(m_4\), and so on. This is called the absorbing phase.

4. After injecting all the message blocks, it applies \(f\) again and extracts a block of bits from the state to form the hash. (If you need a longer hash, apply \(p\) again and extract a block.) This is called the squeezing phase.

Because it is a sponge construction, ingesting the input is naturally called absorbing and creating the digest is called squeezing. The sponge is specified with a \(1600\)-bit permutation using different values for \(r\) and \(c\), depending on the security advertised by the different versions of SHA-3.

The random-oracle model (optional)

Hash functions are usually designed so that their digests are unpredictable and random. This is useful because one cannot always prove a protocol to be secure, thanks to one of the security properties of a hash function we talked about (like collision resistance, for example). Many protocols are instead proven in the random-oracle model, where a fictional and ideal participant called a random oracle is used. In this type of protocol, one can send any inputs as requests to that random oracle, which is said to return completely random outputs in response, and like a hash function, giving it the same input twice returns the same output twice.

Proofs in this model are sometimes controversial as we don’t know for sure if we can replace these random oracles with real hash functions (in practice). Yet, many legitimate protocols are proven secure using this method, where hash functions are seen as more ideal than they probably are.

Attacks on hash functions

As said before, there’s always ought to be a hash collision for every hash function due to the pigeonhole principle. A simple but inefficient attack based on this is to generate enough hashes so that the digests will repeat at some point. More concretely, if a hash function \(H\) outputs an \(n\)-bit digest, then after hashing \(2^n + 1\) distinct inputs, there must be a collision.

Birthday attacks

The birthday attack gets its name from the birthday paradox: that in a group of \(23\) people, the probability of two people sharing a birthday exceeds \(50%\).

Let \(H\) be a hash function with \(N = 2^n\) possible outputs. The birthday paradox implies that we can find a collision with only \(O(\sqrt{N})\) elements with probability greater than \(\frac{1}{2}\). We can come up with the following algorithm that does the birthday attack:

1. Choose \(k\) uniformly random messages \(m_1, \dots, m_k\).

2. Compute \(t_i \gets H(m_i)\) for every \(i\).

3. Search for \(i\) and \(j\) such that \(m_i \ne m_j\) and \(H(m_i) = H(m_j)\).

This algorithm would end up requiring \(\sqrt{N} = 2^{n/2}\) hash evaluations and \(n\sqrt{N} = n 2^{n/2}\) memory, which makes it no (asymptotically) better than a naïve brute force attack. However, it is possible to find collisions with less memory using Floyd’s cycle-finding algorithm.

The way this works is that we have two “runners,” aptly named the tortoise and the hare, run on a long circular track (which would be our sequence). Like in the story, the hare runs twice as fast as the tortoise. They start off at the same position and when the hare overtakes the tortoise, we know that the hare has cycled around at least once.

1. Start at an arbitrary \(x_0 = y_0\).

2. Compute \(x_i \gets H(x_{i-1})\) (tortoise), \(y_i \gets H(H(y_{i-1}))\) (hare),

3. If \(x_i = y_i\), then \(x_i\) and \(H(y_{i-1})\) are a hash collision.

Here, the hash function serves as a sort of a pseudorandom generator to generate a pseudorandom sequence, which if it behaves “random enough” it guarantees us that there is a cycle of length \(\sqrt{N}\). Floyd’s algorithm runs in \(O(\sqrt{N})\) time (so still exponential in \(n\)), but now it only consumes \(O(1)\) memory, which makes it a massive improvement.

Dictionary attacks

Simply put, a dictionary attack is a form of brute force, but it only deals with a limited set of possible inputs. This includes words in a dictionary or previously used passwords acquired from a data breach (such as the rockyou passwords list).

Since a frequent application of cryptographic hash functions is to store passwords securely, password-cracking software such as Hashcat and John the Ripper typically use dictionary attacks, relying on the fact that people mostly use weak and easy-to-guess passwords.

A speed-up of dictionary attack is through a time–memory trade-off technique, where the hashes of dictionary words are precomputed and storing these in a database using the hash as the key. Most websites that “crack” hashes are simply using precomputed tables, while software such as RainbowCrack uses rainbow tables, which reduce storage requirements at the cost of slightly longer lookup times.

References

• Aumasson, Jean-Philippe. 2017. Serious Cryptography: A Practical Introduction to Modern Encryption. No Starch Press.

• Wong, David. 2021. Real-World Cryptography. Manning Publications.