Digital signature schemes

Relevant readings: Katz and Lindell 13.1–13.5, Wong 7.3

Digital signatures

Digital signatures vs. MACs

There are two important properties that digital signatures have, which makes them more preferable to MACs in some cases.

First, signatures are publicly verifiable. Recall that since MACs use the same (secret) key to generate a MAC and to verify a MAC, tag verification can only be done by the key holder. Contrast that to signatures, where anyone with the public key can verify a signature.

Second, signatures are non-repudiable. The main idea of non-repudiation is that the signer cannot (easily) deny issuing a signature. In particular contexts, such as for legal applications, non-repudiation is very crucial. MACs cannot provide this functionality!

Digital signatures vs. public-key encryption

It’s tempting to see signatures as the converse of encryption, but they are not. Signing is not the same as encrypting with the private key. Encryption provides confidentiality whereas a digital signature is used to prevent forgeries. The most salient example of this difference is that it’s okay for a signature scheme to leak information on the message signed, because the message is not secret. For example, a scheme that reveals parts of the messages could be a secure signature scheme but not a secure encryption scheme.

Due to the processing overhead required, public-key encryption can only process short messages, which are usually secret keys rather than actual messages. A signature scheme, however, can process messages of arbitrary sizes by using their hash values \(H(m)\) as a proxy (this is the “hash-and-sign” paradigm), and it can be deterministic yet secure.

Security notions for signature schemes

Like MACs, the general security goal of a digital signature is to prevent signature forgery on a new message.

The security notions EUF-CMA (“secure”) and SUF-CMA (“strongly secure”) carry over from MACs, though we need to tweak their definitions a bit.

Fix a signature scheme \(\Pi = (\textsf{Gen}, \textsf{Sign}, \textsf{Ver})\), a security parameter \(n\), and a PPT adversary \(\mathcal{A}\). We define the EUF-CMA game as follows:

1. \(\Gen{\texttt{1}^n}\) is run to generate keys \((\pk, \sk)\).

2. The adversary \(\mathcal{A}\) is given \(\pk\) and oracle access to \(\Sign{\sk}{\cdot}\). The adversary eventually outputs \((m, \sigma)\).

3. \(\mathcal{A}\) wins if and only if \(\Ver{\pk}{m, \sigma} = \texttt{1}\) and \(\mathcal{A}\) never queried \(m\).

RSA-based signatures

RSA can be repurposed as a signature scheme. If you understood how RSA encryption works, then this section should be straightforward because signing with RSA is the opposite of encrypting with RSA:

• To sign, you encrypt the message with the private key (instead of the public key), which produces a signature (a random element in the group).

• To verify a signature, you decrypt the signature with the public key (instead of the private key). If it gives you back the original message, then the signature is valid.

Textbook RSA signatures

More precisely, if your private key is the private exponent \(d\), and your public key is the public exponent \(e\) and public modulus \(N\), you can:

• Sign a message by computing \(\sigma \gets m^d \bmod N\), and

• Verify a signature by computing \(\sigma^e \bmod N\) and check that it is equal to the message \(m\).

Like with textbook RSA encryption, textbook RSA signatures are also insecure, owing to its malleability. As such, we can do the following sorts of attacks against textbook RSA signatures:

• Forgery from public key

  Choose arbitrary value \(\sigma\), then output \((m, \sigma)\) where \(m \gets \sigma^e \bmod N\).

• Arbitrary forgery for any \(m\)

  Pick \(r\), then compute \(m^\prime \gets r^e m \bmod N\). Query signature for \(m^\prime\): \(\sigma^\prime \gets (r^e m)^d \bmod N = rm^d\). Output \((m, \sigma^\prime r^{-1} \bmod N)\).

Hash-and-sign paradigm

Instead of signing the message itself, we sign the hash of the message. This additional step allows signing of arbitrary-length messages (even beyond what’s supported by the RSA modulus), and protects against signature forgery.

Given a secure signature scheme \(\Pi = (\textsf{Gen}, \textsf{Sign}, \textsf{Ver})\) and a collision-resistant hash function \(H\), we can construct a new signature scheme \(\Pi^\prime = (\textsf{Gen}, \textsf{Sign}^\prime, \textsf{Ver}^\prime)\) as follows:

• \(\textsf{Sign}^\prime\): \(\sigma \gets \Sign{\sk}{H(m)}\)

• \(\textsf{Ver}^\prime\): output 1 if \(\Ver{\pk}{H(m), \sigma} = \texttt{1}\), 0 otherwise

The nice thing about this construction is that if our original signature scheme \(\Pi\) is secure and the hash function \(H\) is collision-resistant, then our new signature scheme \(\Pi^\prime\) is also secure.

RSA PKCS #1 v1.5

We have already seen the PKCS #1 v1.5 standard in the context of RSA encryption, but this same document contained a specification for signing with RSA. The signature scheme standardized in that document is pretty much the same as the encryption scheme. To sign, first hash the message with a hash function of your choice, then pad it according to PKCS#1 v1.5’s padding for signatures (which is similar to the padding for encryption in the same standard). Next, encrypt the padded and hashed message with your private exponent. Figure 1 illustrates this process.

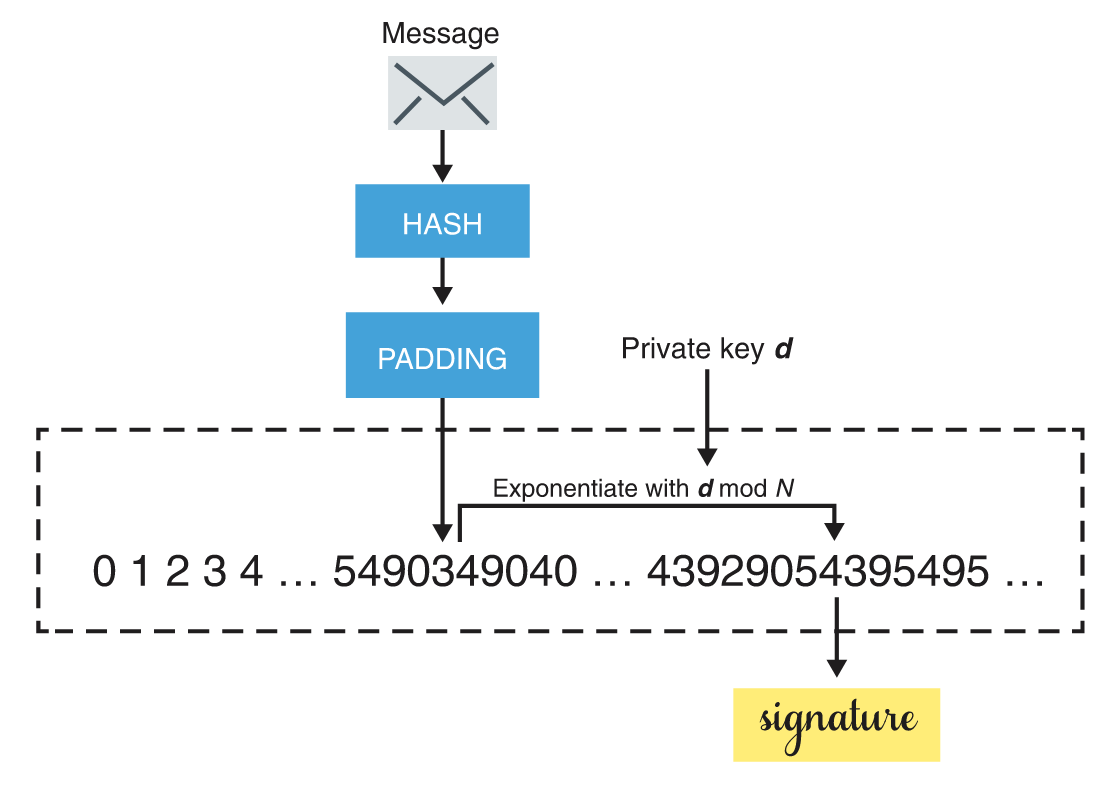
It was mentioned earlier that there were damaging attacks on RSA PKCS#1 v1.5 for encryption; the same is unfortunately true for RSA PKCS#1 v1.5 signatures. In 1998, after Bleichenbacher found a devastating attack on RSA PKCS#1 v1.5 for encryption, he decided to take a look at the signature standard. Bleichenbacher came back in 2006 with a signature forgery attack on RSA PKCS#1 v1.5, one of the most catastrophic types of attack on signatures — attackers can forge signatures without knowledge of the private key! Unlike the first attack that broke the encryption algorithm directly, the second attack was an implementation attack. This meant that if the signature scheme was implemented correctly (according to the specification), the attack did not work.

Unfortunately, RSA PKCS#1 v1.5 for signatures is still widely used. Be aware of these issues if you really have to use this algorithm for backward compatibility reasons. Having said that, this does not mean that RSA for signatures is insecure.

RSA-FDH

The main idea behind Full Domain Hash (FDH) is pretty straightforward: apply a “cryptographic transformation” to messages before signing. This could be done, for example, by applying a cryptographic hash function to the message; as such, it is just a direct application of the hash-and-sign paradigm. To implement it, you simply convert the byte string \(H(m)\) to a number, \(x\), and create the signature \(\sigma \gets x^d \bmod N\). Signature verification is straightforward, too. Given a signature \(\sigma\), you compute \(x' \gets \sigma^e \bmod N\) and compare the result with \(H(m)\).

As the name implies, the hash function used must map onto all possible values of \(\ZZ_N^*\), or in other words, the range of the hash function must be large enough to cover the entire domain of the RSA modulus.

RSA-PSS

The RSA Probabilistic Signature Scheme (PSS) is to RSA signatures what OAEP is to RSA encryption. It was designed to make message signing more secure, thanks to the addition of padding data.

RSA-PSS was standardized in the updated PKCS#1 v2.1 and included a proof of security (unlike the signature scheme standardized in the previous PKCS#1 v1.5). The newer specification (shown in Figure 2) works like this:

• Encode the message using the PSS encoding algorithm.

• Sign the encoded message using RSA (as was done in the PKCS#1 v1.5 standard).

Verifying a signature produced by RSA-PSS is just a matter of inverting the encoding once the signature has been raised to the public exponent modulo the public modulus.

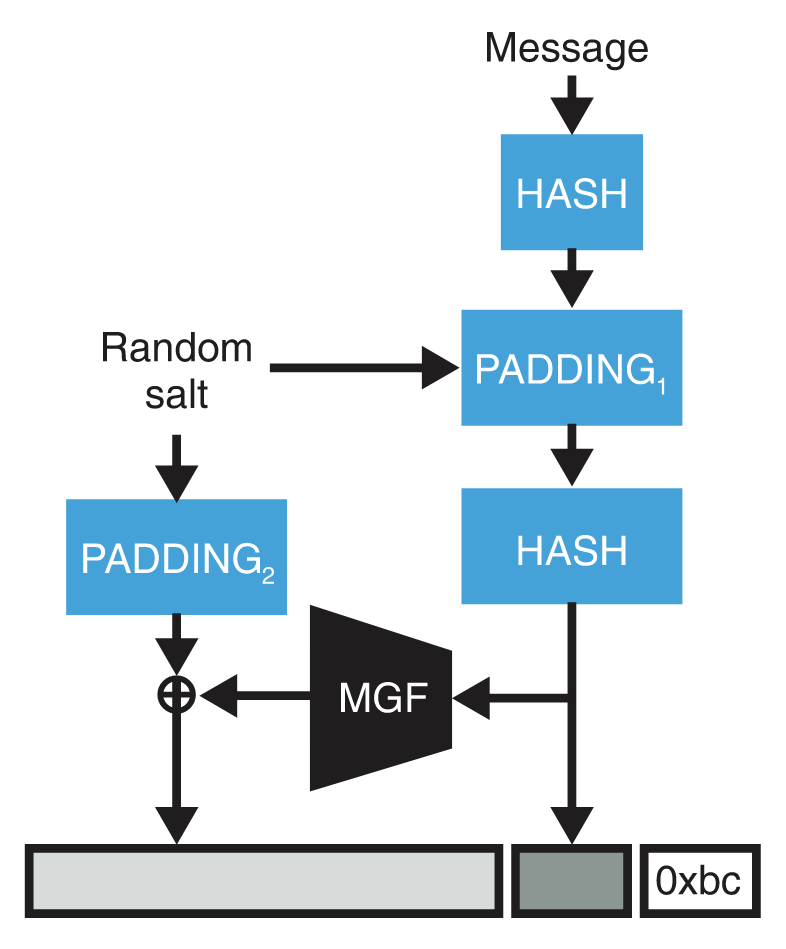
PSS is provably secure, meaning that no one should be able to forge a signature without knowledge of the private key. Instead of proving that if RSA is secure then RSA-PSS is secure, RSA-PSS proves the contrapositive: if someone can break RSA-PSS then that someone can also break RSA. Of course, this only works if RSA is secure, which we assume in the proof.

Compared to FDH, PSS is more complicated, so why bother with the complexity of PSS? The main reason is that PSS was released after FDH, in 1996, and it has a security proof that inspires more confidence than FDH. Specifically, its proof offers slightly higher security guarantees than the proof of FDH, and its use of randomness helped strengthen that proof. These stronger theoretical guarantees are the main reason cryptographers prefer PSS over FDH, but most applications using PSS today could switch to FDH with no meaningful security loss. In some contexts, however, a viable reason to use PSS instead of FDH is that PSS’s randomness protects it from some attacks on its implementation.

Authenticated key exchange

We saw different ways to perform key exchanges between two participants, and we learned that these key exchanges are useful to negotiate a shared secret, which can then be used to secure communications with an authenticated encryption algorithm. Yet, key exchanges didn’t fully solve the problem of setting up a secure connection between two participants as an active man-in-the-middle (MITM) attacker can trivially impersonate both sides of a key exchange. This is where signatures enter the ring.

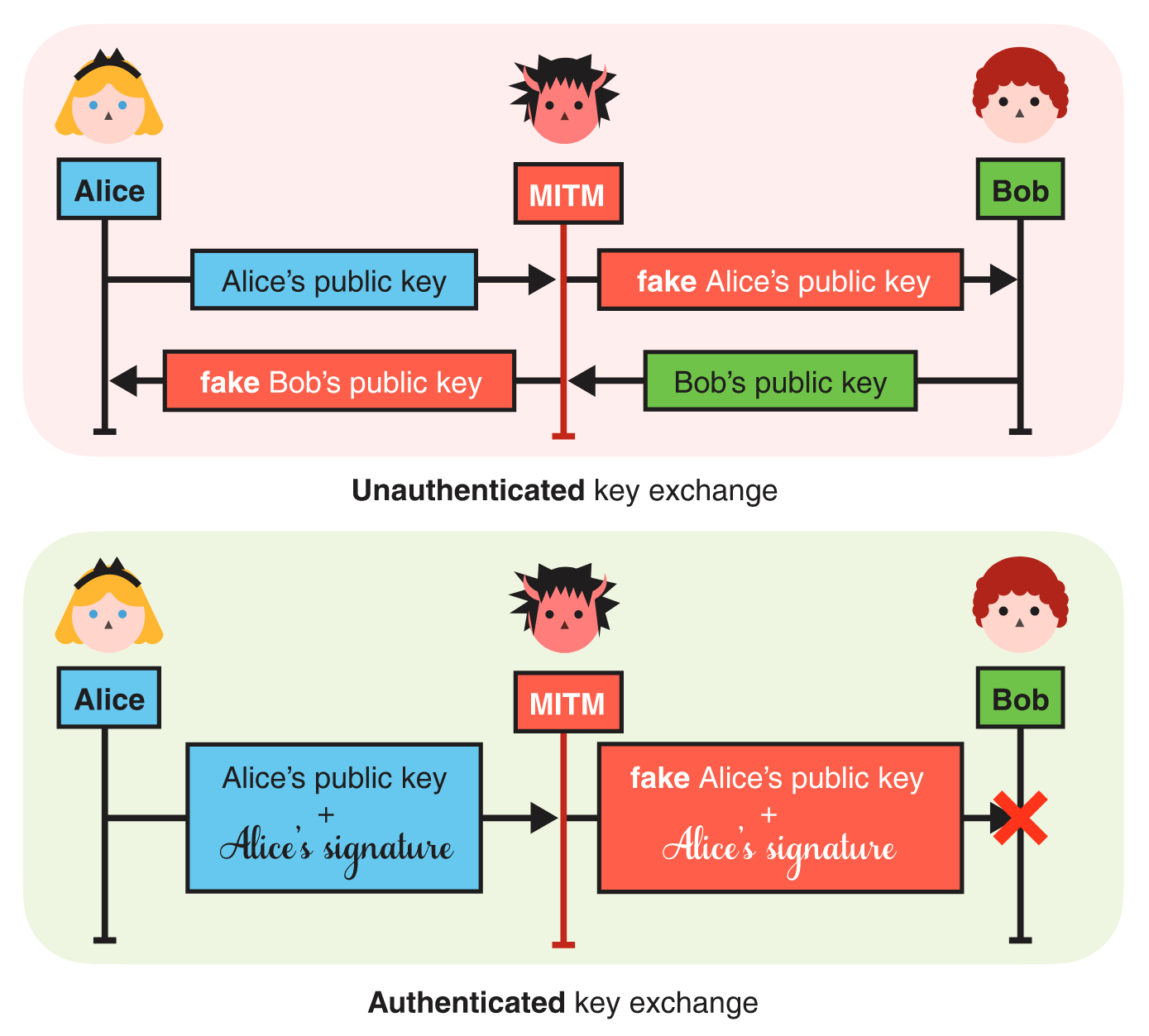
Imagine that Alice and Bob are trying to set up a secure communication channel between themselves and that Bob is aware of Alice’s verifying key. Knowing this, Alice can use her signing key to authenticate her side of the key exchange: she generates a key exchange key pair, signs the public key part with her signing key, then sends the key exchange public key along with the signature. Bob can verify that the signature is valid using the associated verifying key he already knows and then use the key exchange public key to perform a key exchange.

We call such a key exchange an authenticated key exchange. If the signature is invalid, Bob can tell someone is actively MITM’ing the key exchange. Figure 3 shows a comparison between an unauthenticated and an authenticated key exchange.

Note that in this example, the key exchange is only authenticated on one side: while Alice cannot be impersonated, Bob can. If both sides are authenticated (i.e., Bob would sign his part of the key exchange), we call the key exchange a mutually-authenticated key exchange.

References

• Wong, David. 2021. Real-World Cryptography. Manning Publications.