RSA

Relevant readings: Aumasson ch. 10, Katz and Lindell 12.5, Wong 6.3

RSA encryption

Textbook RSA

We first describe the simplest form of RSA called “textbook RSA.” By itself it is insecure, but it serves as a stepping stone for more secure schemes that are actually used in practice.

Let GenRSA be a PPT algorithm that, given \(\texttt{1}^n\), outputs a modulus \(N\) that is the product of two \(n\)-bit primes, along with integers \(e,d\) satisfying \(ed \equiv 1 \pmod{\phi(N)}\). We use an algorithm called GenModulus as a subroutine that outputs a composite modulus \(N\) along with its factorization.

We can implement GenModulus in SageMath using the random_prime function to generate primes:¹

As random_prime verifies if the generated prime is actually prime, this can potentially slow down our rsa_genmodulus function, so we supply an additional parameter proof=False to random_prime to skip this verification step.

Suppose \(N, e, d\) are defined as above, and let \(c = m^e \bmod N\) for some \(m \in \ZZ_N^*\). RSA encryption works because someone who has \(d\) can recover \(m\) from \(c\) by computing \(c^d \bmod N\), since: $$c^d = \left(m^e\right)^d = m^{ed} \equiv m \pmod{N}.$$ If \(d\) is not known, then the RSA assumption (from Lecture 5) says that it is difficult to recover \(m\) from \(c\) even if \(N\) and \(e\) are known. In this sense, computing \(m^e \bmod N\) is a trapdoor and \(d\) is the ladder that we use to get out. We define the textbook RSA scheme as follows:

• Gen: given \(\texttt{1}^n\) run to obtain \(N\), \(e\), and \(d\). The public key is \((N, e)\) and the private key is \((N, d)\).

• Enc: given a public key \(\pk = (N, e)\) and a message \(m \in \ZZ_N^*\), compute the ciphertext $$c \gets m^e \bmod N.$$

• Dec: given a private key \(\sk = (N, d)\) and a ciphertext \(c \in \ZZ_N^*\), compute the message $$m \gets c^d \bmod N.$$

Since Enc is deterministic (notice that we don’t use any randomness for encryption), it is not CPA-secure.

Padded RSA

To make textbook RSA CPA-secure, we need encryption to be nondeterministic (i.e., randomized). One way to do this is to randomly pad the message before encrypting. More concretely, to map a message \(m\) to an element of \(\ZZ_N^\), the sender chooses a uniform bit-string \(r \in \Set{\texttt{0}, \texttt{1}}^\ell\) (for some appropriate \(\ell\)) and sets \(\hat{m} \gets r \mathrel{\hspace{1pt}||\hspace{1pt}}m\); the resulting value can naturally be interpreted as an integer in \(\ZZ_N^\). We can see that this mapping is reversible, as we can simply chop off the extra bits after decryption.

Let GenRSA be as before, and let \(\ell\) be a function with \(\ell(n) < 2n\). We define the padded RSA scheme as follows:

• Gen: given \(\texttt{1}^n\) run to obtain \(N\), \(e\), and \(d\). The public key is \((N, e)\) and the private key is \((N, d)\).

• Enc: given a public key \(\pk = (N, e)\) and a message \(m \in \Set{\texttt{0}, \texttt{1}}^{q - \ell(n) - 1}\) (where \(N\) is \(q\) bits long), choose a string \(r \in \Set{\texttt{0}, \texttt{1}}^\ell\) and interpret \(\hat{m} \gets r \mathrel{\hspace{1pt}||\hspace{1pt}}m\) as an element of \(\ZZ_N^*\), then compute the ciphertext $$c \gets \hat{m}^e \bmod N.$$

• Dec: given a private key \(\sk = (N, d)\) and a ciphertext \(c \in \ZZ_N^*\), compute the message $$\hat{m} \gets c^d \bmod N,$$ and output the \(q - \ell(n) - 1\) least significant bits of \(\hat{m}\).

PKCS#1 v1.5

The PKCS#1 v1.5 standard, published in 1993, defines a variant of padded RSA. For a public key \(\pk = (N, e)\), let \(k\) denote the length of \(N\) in bytes. We assume that a message \(m\) to be encrypted has a length an integer number of bytes ranging from \(1\) to \(k-11\). Encryption of a \(D\)-byte message \(m\) is computed as $$(\texttt{0x00} \mathrel{\hspace{1pt}||\hspace{1pt}}\texttt{0x02} \mathrel{\hspace{1pt}||\hspace{1pt}}r \mathrel{\hspace{1pt}||\hspace{1pt}}\texttt{0x00} \mathrel{\hspace{1pt}||\hspace{1pt}}m)^e \bmod N,$$ where \(r\) is a randomly generated \((k-D-3)\)-byte string with none of its bytes equal to 0x00.

Since a devastating chosen-ciphertext attack due to Bleichenbacher has been demonstrated against PKCS#1 v1.5, newer versions of the standard have been introduced.²

RSA-OAEP and PKCS#1 v2

A bigger problem with textbook RSA is that it is malleable. In this case, given the encryption \(c = m^e \bmod N\) of some unknown message \(m\), it’s easy to generate a related ciphertext \(c^\prime\) that is an encryption of \(2m \bmod N\) by setting: $$c^\prime \gets 2^e \cdot c \bmod N = 2^e \cdot m^e = (2m)^e \bmod N.$$ In fact, if we have two ciphertexts \(c_1 = m_1^e \bmod N\) and \(c_2 = m_2^e \bmod N\), we can derive the ciphertext of \(c_1 \cdot c_2\) by multiplying these two ciphertexts together, like this: $$(c_1 \cdot c_2) \bmod N = (m_1^e \cdot m_2^e) \bmod N = (m_1 \cdot m_2)^e \bmod N.$$ Thus we now have the ciphertext of the message \(m_1 \cdot m_2\).

In order to make RSA ciphertexts nonmalleable, the ciphertext should consist of the message data and some padding. Another way of padding the message is the optimal asymmetric encryption padding (OAEP), commonly referred to as RSA-OAEP, which is standardized as part of the PKCS#1 v2 standard. This scheme involves creating a bit string as large as the modulus by padding the message with extra data and randomness before applying the RSA function. Unlike its predecessor, PKCS#1 v1.5, OAEP is not vulnerable to Bleichenbacher’s attack and is, thus, a strong standard to use for RSA encryption nowadays. Let’s see how OAEP works and prevents the previously discussed attacks.

Like most cryptographic algorithms, OAEP comes with a key-generation algorithm, which takes the security parameter \(\texttt{1}^n\) as input. As with Diffie–Hellman, operations happen in the ring of integers modulo a large number. When we talk about the security of an instantiation of RSA, we usually refer to the size of that large modulus. This is similar to Diffie–Hellman if you remember.

To encrypt, the algorithm first pads the message and mixes it with a random number generated per encryption. The result is then encrypted with RSA. To decrypt the ciphertext, the process is reversed as Figure 1 shows. RSA-OAEP uses this mixing in order to make sure that if a few bits of what is encrypted with RSA leak, no information on the plaintext can be obtained. Indeed, to reverse the OAEP padding, you need to obtain (close to) all the bytes of the OAEP padded plaintext! In addition, Bleichenbacher’s attack should not work anymore because the scheme makes it impossible to obtain well-formed plaintext by modifying a ciphertext.

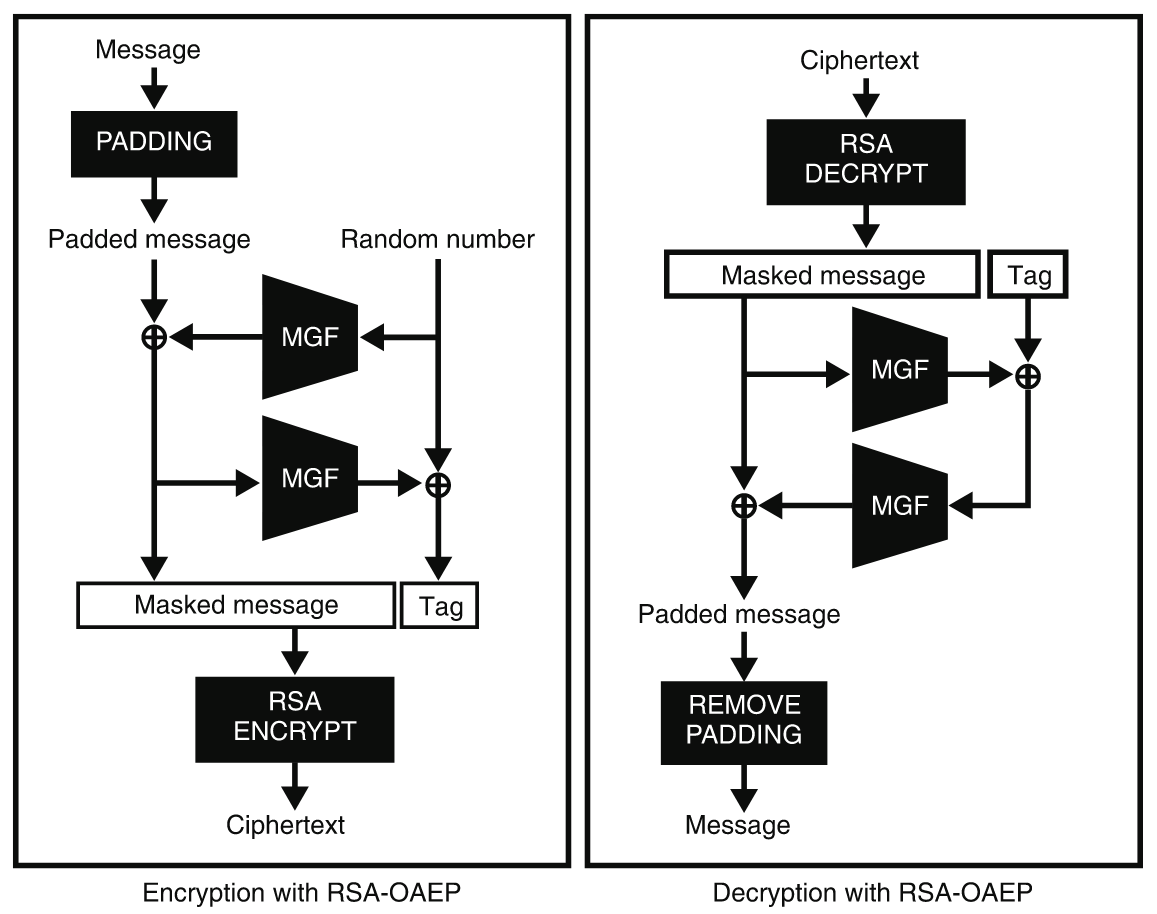
Inside of OAEP, MGF stands for mask generation function. MGFs are built using a hash function that hashes the input repeatedly with a counter (sort of like “a hash function in CTR mode”).

The takeaway here is that always use OAEP whenever you use RSA. Nowadays, most protocols and applications that use RSA either still implement the insecure PKCS#1 v1.5 or OAEP. On the other hand, more and more protocols are moving away from RSA encryption in favor of elliptic curve Diffie–Hellman (ECDH). for both key exchanges and hybrid encryption. This is understandable as ECDH provides shorter public keys and benefits, in general, from much better standards and much safer implementations.

Implementing RSA

In practice, you do not (and should not) have to implement RSA from scratch. You always use a library that cryptographers have developed, refined, and field-tested over the years. For example, we use the cryptography library in Python, which supports RSA operations.³

Nonetheless, it is still important to be aware of possible issues and concerns arising from implementing RSA.

Small exponents for faster encryption/decryption

The speed of encryption and decryption heavily depends on the speed of modular exponentiation. Smaller exponents (to be more precise, exponents with fewer set bits in their binary representation) require fewer multiplications and therefore can make the exponentiation computation much faster.

We are not actually limited on what values we can use for the public exponent \(e\); just that it should be between \(3\) and \(\phi(N)-1\), and that \(e\) and \(\phi(N)\) are relatively prime. But in practice, we typically use \(e = 3\), \(e = 17\), or \(e = 65537\). What’s so special about these values? If we convert them into binary, we get: $$\begin{align} 3 &= \texttt{11} \\ 17 &= \texttt{10001} \\ 65537 &= \texttt{10000000000000001}\end{align}$$ These numbers are called Fermat primes, because they are primes that can be written in the form \(2^{2^p} + 1\), which explains why there are only two set bits (namely one for \(1\) and another for \(2^{2^p}\)). In particular, \(65537\) is the fourth Fermat prime \(F_4\), which is why OpenSSL has a flag called -F4 that tells it to use \(e = 65537\) when generating RSA keys.

Using \(e=3\) makes RSA susceptible to a low-exponent attack (which we’ll discuss later) so we just always use \(e = 65537\) to be safe.

Using the Chinese remainder theorem

One way to speed up decryption in RSA is by using the Chinese remainder theorem to operate in the groups \(\ZZ_p^\) and \(\ZZ_q^\) instead of the much larger \(\ZZ_N^*\). Rather than computing \(c^d \bmod N\), we first compute: $$\begin{align} d_p &\gets e^{-1} \bmod (p-1) \\ d_q &\gets e^{-1} \bmod (q-1) \\ q^\prime &\gets q^{-1} \bmod p\end{align}$$ Thus your private key is now a quintuple \((p, q, d_p, d_q, q^\prime)\) instead of the pair \((N, d)\).⁴ To decrypt a ciphertext \(c\), we compute: $$\begin{align} m_1 &\gets (c^d \bmod N) \bmod p = ((c \bmod p)^{d_p}) \bmod p \\ m_2 &\gets (c^d \bmod N) \bmod q = ((c \bmod q)^{d_q}) \bmod q\end{align}$$ Then we “recombine” them by finding \(m\) such that: $$\begin{align} m &\equiv m_1 \pmod{p} \\ m &\equiv m_2 \pmod{q}\end{align}$$ Thus the Chinese remainder theorem says that there’s a unique solution for \(m\) modulo \(pq\), which is: $$m= m_1 \cdot q \cdot q^\prime + m_2 \cdot p \cdot (p^{-1} \bmod q).$$

Some attacks on RSA

Most of the attacks presented here are covered in Dan Boneh’s paper “Twenty Years of Attacks on the RSA Cryptosystem” which reviews and explains the most important attacks on RSA (Boneh 1999).

Weak RSA keys

RSA is only as strong as the keys being used. Even though the key length is long enough to make factoring the keys infeasible, a bug in the random number generator may result in the prime number generator to produce weak keys, which could snowball into two public keys whose moduli share a prime factor! Unfortunately, this happens all too often in real-world applications, as this paper had found out (Heninger et al. 2012).

Consider two public keys \((N_1, e_1)\) and \((N_2, e_2)\). If both moduli share a prime factor, then we can easily recover it by computing \(p \gets \gcd(N_1, N_2)\). Then recovering the other factor of each modulus is trivial: $$q_1 \gets N_1/p \quad\text{and}\quad q_2 \gets N_2/p.$$ Once you have \(p, q_1, q_2\), then it’s game over, as we can easily recover the private exponents from those values.

Håstad’s broadcast attack

Another popular optimization of RSA is to use a small public exponent, namely \(e = 3\), which is supposed to make encryption and decryption very fast. However, if the message \(m\) is too small for a “reduction modulo \(N\)” to have an effect, i.e., when \(m < N^{1/3}\), then the value of \(m^3\) in \(\ZZ_N\) is the same as the value of \(m^3\) in \(\ZZ\). Thus we can recover \(m\) from \(m^3\) by simply getting the cube root of \(m\) over the integers.

Suppose a message \(m\) was encrypted with three different \(1024\)-bit RSA public keys, all of which have the exponent \(e=3\) and different (pairwise relatively prime) moduli \(N_1, N_2, N_3\), resulting in three ciphertexts \(c_1, c_2, c_3\). These ciphertexts are computed as: $$\begin{align} c_1 &= m^3 \bmod N_1 \\ c_2 &= m^3 \bmod N_2 \\ c_3 &= m^3 \bmod N_3\end{align}$$

Then an adversary can recover the message \(m\) even without factoring the moduli or recovering the private key, due to an attack by Håstad:⁵

1. The adversary gets a hold of the ciphertexts \(c_1, c_2, c_3\) and the moduli \(N_1, N_2, N_3\).

2. It then considers the system of linear congruences: $$\begin{align} x &\equiv c_1 \equiv m^3 \pmod{N_1} \\ x &\equiv c_2 \equiv m^3 \pmod{N_2} \\ x &\equiv c_3 \equiv m^3 \pmod{N_3} \end{align}$$ Use the Chinese remainder theorem to solve this system to find the solution \(c\) modulo \(N_1 N_2 N_3\). It then knows that \(c = m^3 \bmod N_1 N_2 N_3\).

3. Now since \(m^3 < N_1 N_2 N_3\), the adversary can take the cube root of \(c\) (over the integers) to recover \(m\), i.e., \(m = \sqrt[3]{c}\).

Bleichenbacher’s million message attack

While the PKCS#1 standard fixes some known issues, in 1998, Bleichenbacher found a practical attack on PKCS#1 v1.5 that allowed an attacker to decrypt messages encrypted with the padding specified by the standard. As it required a million messages, it is infamously called the million message attack. Mitigations were later found, but interestingly, over the years, the attack has been rediscovered again and again as researchers found that the mitigations were too hard to implement securely (if at all).

Bleichenbacher’s million message attack is a type of an adaptive chosen-ciphertext attack (CCA2). CCA2 means that to perform this attack, an attacker can submit arbitrary RSA encrypted messages, observe how it influences the decryption, and continue the attack based on previous observations (the adaptive part).

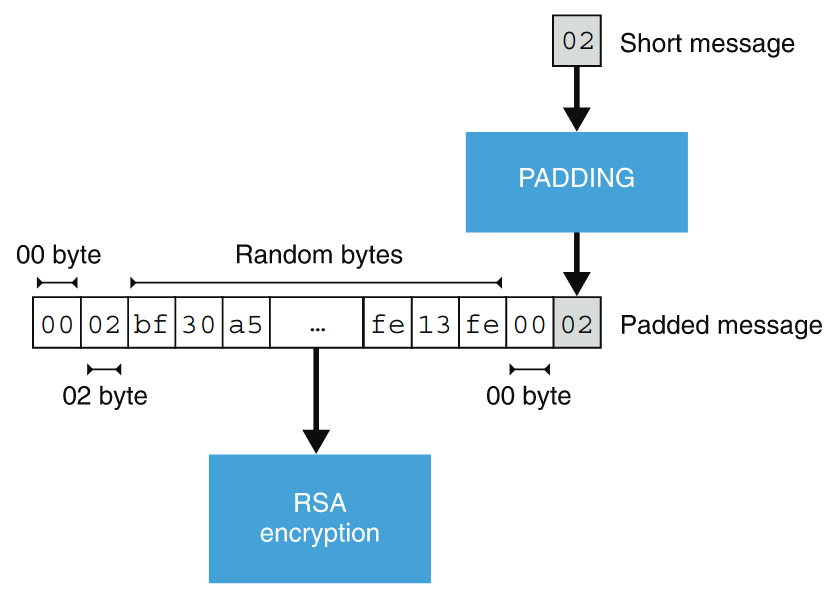
Bleichenbacher made use of the malleability property of RSA in his million message attack on RSA PKCS#1 v1.5. His attack works by intercepting an encrypted message, modifying it, and sending it to the person in charge of decrypting it. By observing if that person can decrypt it (the padding remained valid), we obtain some information about the message range. Because the first two bytes are 0x0002, we know that the decryption is smaller than some value. By doing this iteratively, we can narrow that range down to the original message itself.

Even though Bleichenbacher’s attack is well-known, there are still many systems in use today that implement RSA PKCS#1 v1.5 for encryption, and so variants of this vulnerability still exist in many modern servers, now known as the “Return Of Bleichenbacher’s Oracle Threat” (ROBOT) attack.⁶

References

• Aumasson, Jean-Philippe. 2017. Serious Cryptography: A Practical Introduction to Modern Encryption. No Starch Press.

• Boneh, Dan. 1999. "Twenty Years of Attacks on the RSA Cryptosystem." Notices of the American Mathematical Society 46 (2): 203--13.

• Heninger, Nadia, Zakir Durumeric, Eric Wustrow, and J. Alex Halderman. 2012. "Mining Your Ps and Qs: Detection of Widespread Weak Keys in Network Devices." In Proceedings of the 21st USENIX Security Symposium.

• Katz, Jonathan, and Yehuda Lindell. 2021. Introduction to Modern Cryptography. 3rd ed. CRC Press.

• Wong, David. 2021. Real-World Cryptography. Manning Publications.